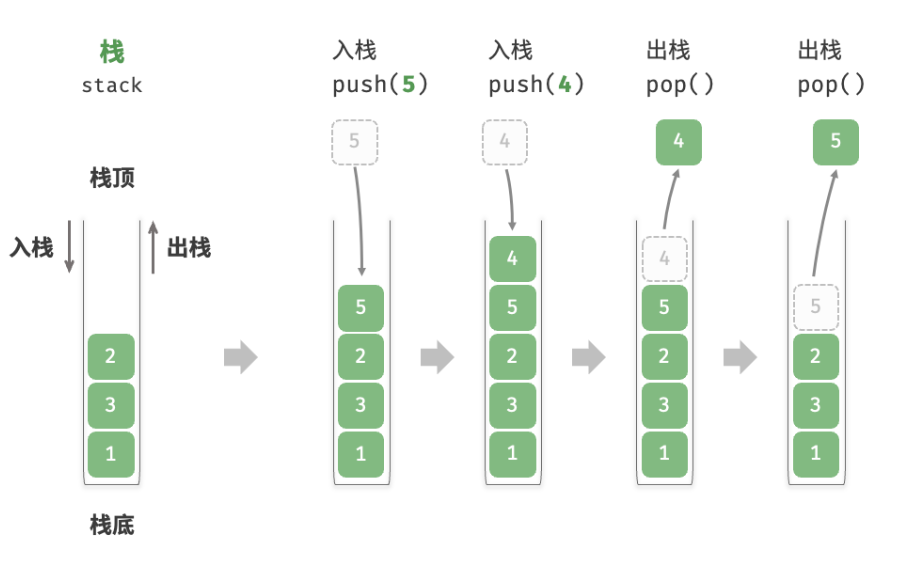
栈 栈是一种遵循先入后出的逻辑的线性数据结构。如下图所示,我们把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。将把元素添加到栈顶的操作叫做“入栈”,删除栈顶元素的操作叫做“出栈”。
栈常用操作 栈的常用操作如下表所示,具体的方法名需要根据所使用的编程语言来确定。在此,我们以常见的 push()、pop()、peek() 命名为例。
表 栈的操作效率
方法
描述
时间复杂度
push()
元素入栈(添加至栈顶)
O(1)
pop()
栈顶元素出栈
O(1)
peek()
访问栈顶元素
O(1)
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 stack: list [int ] = [] stack.append(1 ) stack.append(3 ) stack.append(2 ) stack.append(5 ) stack.append(4 ) peek: int = stack[-1 ] pop: int = stack.pop() size: int = len (stack) is_empty: bool = len (stack) == 0
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 var stack []int stack = append (stack, 1 ) stack = append (stack, 3 ) stack = append (stack, 2 ) stack = append (stack, 5 ) stack = append (stack, 4 ) peek := stack[len (stack)-1 ] pop := stack[len (stack)-1 ] stack = stack[:len (stack)-1 ] size := len (stack) isEmpty := len (stack) == 0
栈的实现 栈遵循先入后出的原则,因此我们只能在栈顶添加或删除元素。然而,数组和链表都可以在任意位置添加和删除元素,因此栈可以被视为一种受限制的数组或链表 。
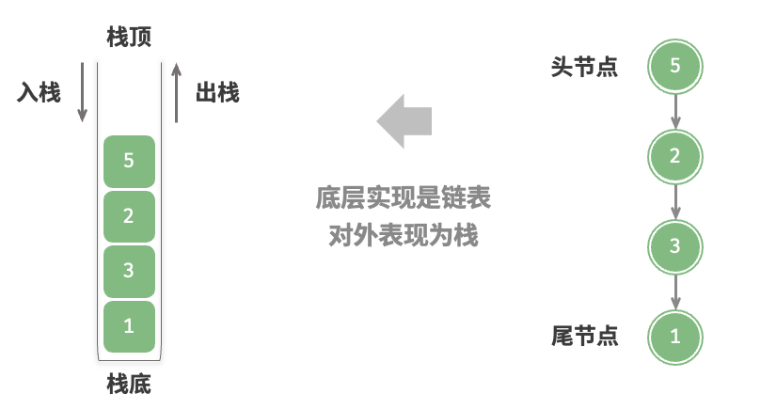
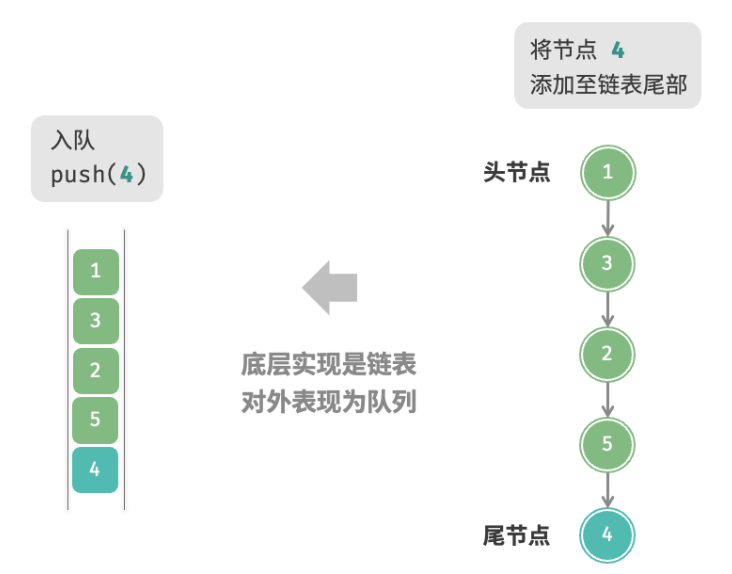
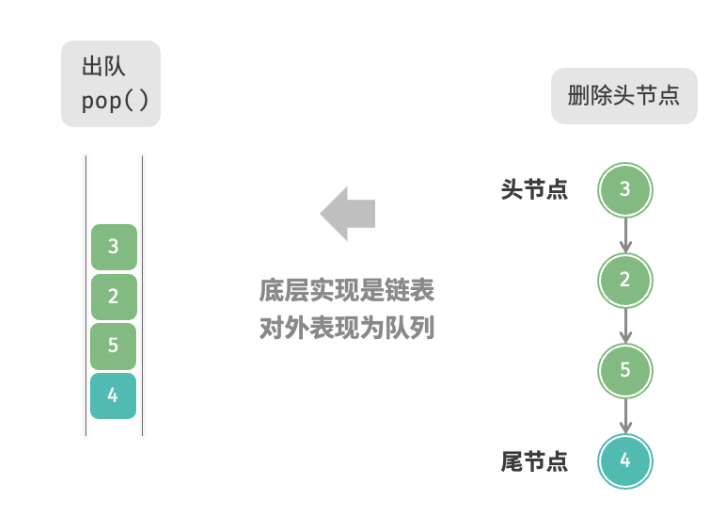
基于链表的实现 使用链表来实现栈时,我们可以将链表的头节点视为栈顶,尾节点视为栈底。
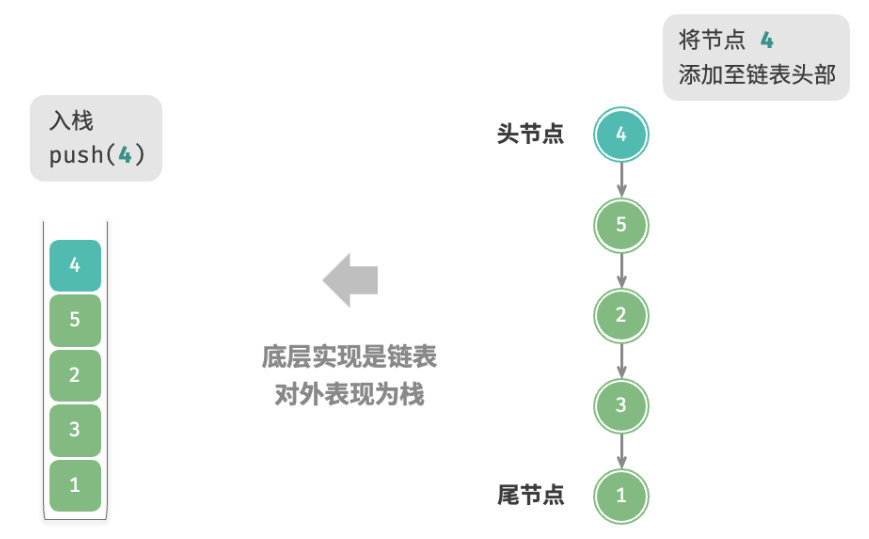
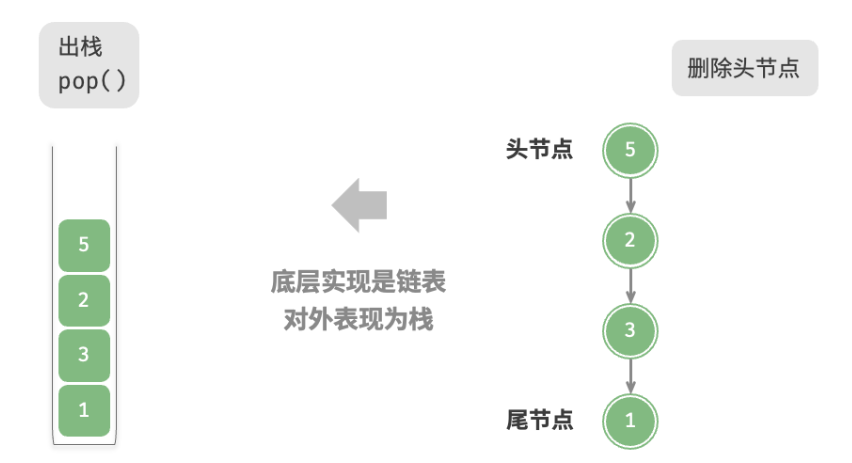
如下图所示,对于入栈操作,我们只需将元素插入链表头部,这种节点插入方法被称为“头插法”。而对于出栈操作,只需将头节点从链表中删除即可。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class LinkedListStack : """基于链表实现的栈""" def __init__ (self ): """构造方法""" self.__peek: ListNode | None = None self.__size: int = 0 def size (self ) -> int : """获取栈的长度""" return self.__size def is_empty (self ) -> bool : """判断栈是否为空""" return not self.__peek def push (self, val: int ): """入栈""" node = ListNode(val) node.next = self.__peek self.__peek = node self.__size += 1 def pop (self ) -> int : """出栈""" num: int = self.peek() self.__peek = self.__peek.next self.__size -= 1 return num def peek (self ) -> int : """访问栈顶元素""" if not self.__peek: return None return self.__peek.val def to_list (self ) -> list [int ]: """转化为列表用于打印""" arr = [] node = self.__peek while node: arr.append(node.val) node = node.next arr.reverse() return arr
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 type linkedListStack struct { data *list.List } func newLinkedListStack () return &linkedListStack{ data: list.New(), } } func (s *linkedListStack) int ) { s.data.PushBack(value) } func (s *linkedListStack) if s.isEmpty() { return nil } e := s.data.Back() s.data.Remove(e) return e.Value } func (s *linkedListStack) if s.isEmpty() { return nil } e := s.data.Back() return e.Value } func (s *linkedListStack) int { return s.data.Len() } func (s *linkedListStack) bool { return s.data.Len() == 0 } func (s *linkedListStack) return s.data }
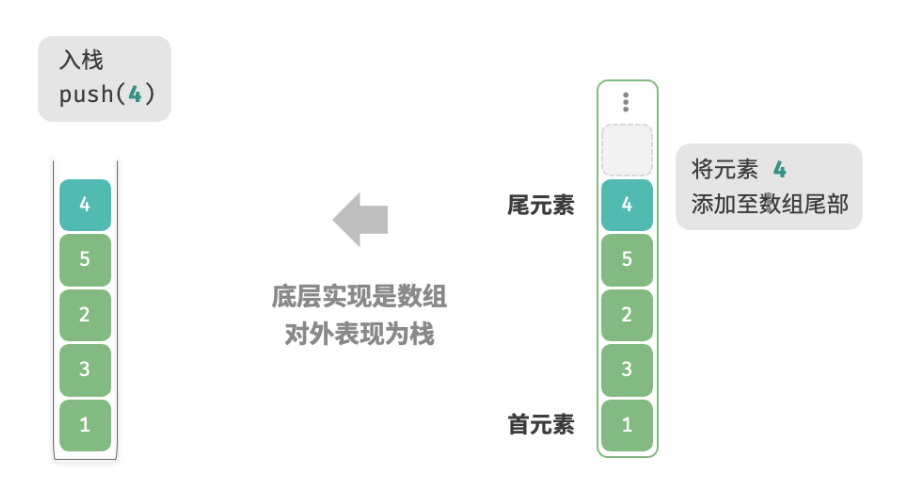
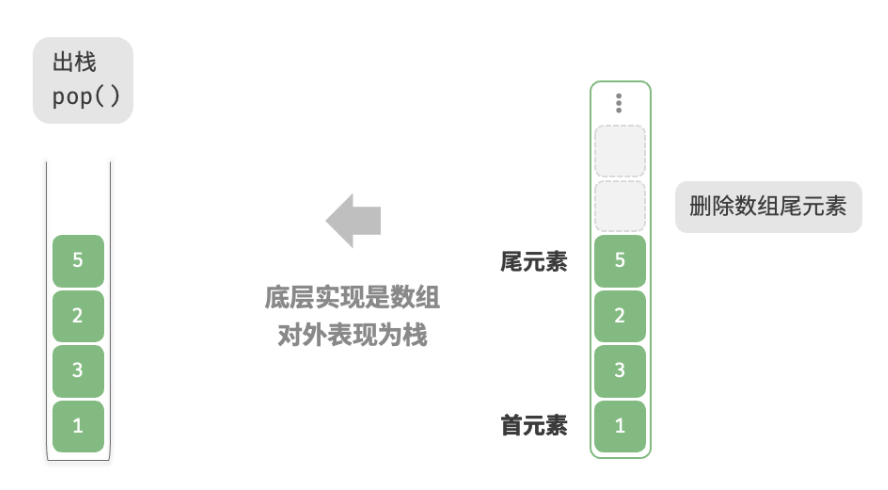
基于数组的实现 使用数组实现栈时,我们可以将数组的尾部作为栈顶。如下图所示,入栈与出栈操作分别对应在数组尾部添加元素与删除元素,时间复杂度都为 O(1)。
由于入栈的元素可能会源源不断地增加,因此我们可以使用动态数组,这样就无须自行处理数组扩容问题。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class ArrayStack : """基于数组实现的栈""" def __init__ (self ): """构造方法""" self.__stack: list [int ] = [] def size (self ) -> int : """获取栈的长度""" return len (self.__stack) def is_empty (self ) -> bool : """判断栈是否为空""" return self.__stack == [] def push (self, item: int ): """入栈""" self.__stack.append(item) def pop (self ) -> int : """出栈""" if self.is_empty(): raise IndexError("栈为空" ) return self.__stack.pop() def peek (self ) -> int : """访问栈顶元素""" if self.is_empty(): raise IndexError("栈为空" ) return self.__stack[-1 ] def to_list (self ) -> list [int ]: """返回列表用于打印""" return self.__stack
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 type arrayStack struct { data []int } func newArrayStack () return &arrayStack{ data: make ([]int , 0 , 16 ), } } func (s *arrayStack) int { return len (s.data) } func (s *arrayStack) bool { return s.size() == 0 } func (s *arrayStack) int ) { s.data = append (s.data, v) } func (s *arrayStack) val := s.peek() s.data = s.data[:len (s.data)-1 ] return val } func (s *arrayStack) if s.isEmpty() { return nil } val := s.data[len (s.data)-1 ] return val } func (s *arrayStack) int { return s.data }
两种实现对比 支持操作
两种实现都支持栈定义中的各项操作。数组实现额外支持随机访问,但这已超出了栈的定义范畴,因此一般不会用到。
时间效率
在基于数组的实现中,入栈和出栈操作都是在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入栈时超出数组容量,会触发扩容机制,导致该次入栈操作的时间复杂度变为 O(n) 。
在链表实现中,链表的扩容非常灵活,不存在上述数组扩容时效率降低的问题。但是,入栈操作需要初始化节点对象并修改指针,因此效率相对较低。不过,如果入栈元素本身就是节点对象,那么可以省去初始化步骤,从而提高效率。
综上所述,当入栈与出栈操作的元素是基本数据类型时,例如 int 或 double ,我们可以得出以下结论。
基于数组实现的栈在触发扩容时效率会降低,但由于扩容是低频操作,因此平均效率更高。
基于链表实现的栈可以提供更加稳定的效率表现。
空间效率
在初始化列表时,系统会为列表分配“初始容量”,该容量可能超过实际需求。并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容,扩容后的容量也可能超出实际需求。因此,基于数组实现的栈可能造成一定的空间浪费 。
然而,由于链表节点需要额外存储指针,因此链表节点占用的空间相对较大 。
综上,我们不能简单地确定哪种实现更加节省内存,需要针对具体情况进行分析。
栈典型应用
浏览器中的后退与前进、软件中的撤销与反撤销 。每当我们打开新的网页,浏览器就会将上一个网页执行入栈,这样我们就可以通过后退操作回到上一页面。后退操作实际上是在执行出栈。如果要同时支持后退和前进,那么需要两个栈来配合实现。程序内存管理 。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。在递归函数中,向下递推阶段会不断执行入栈操作,而向上回溯阶段则会执行出栈操作。
队列 队列是一种遵循先入先出规则的线性数据结构。顾名思义,队列模拟了排队现象,即新来的人不断加入队列的尾部,而位于队列头部的人逐个离开。
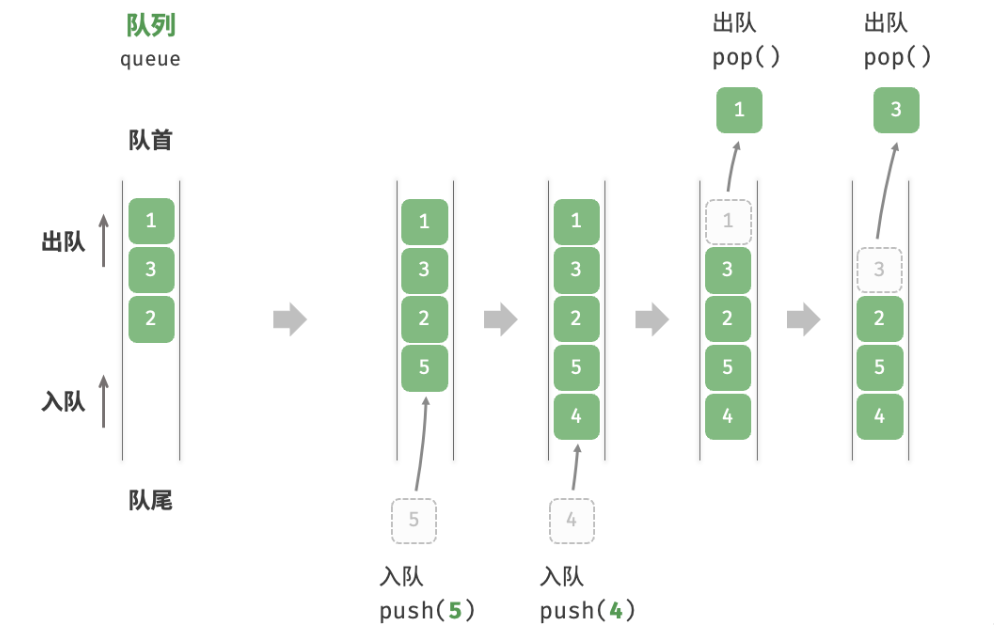
如下图所示,我们将队列的头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。
队列常用操作 表 队列操作效率
方法名
描述
时间复杂度
push()
元素入队,即将元素添加至队尾
O(1)
pop()
队首元素出队
O(1)
peek()
访问队首元素
O(1)
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 que: deque[int ] = collections.deque() que.append(1 ) que.append(3 ) que.append(2 ) que.append(5 ) que.append(4 ) front: int = que[0 ]; pop: int = que.popleft() size: int = len (que) is_empty: bool = len (que) == 0
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 queue := list.New() queue.PushBack(1 ) queue.PushBack(3 ) queue.PushBack(2 ) queue.PushBack(5 ) queue.PushBack(4 ) peek := queue.Front() pop := queue.Front() queue.Remove(pop) size := queue.Len() isEmpty := queue.Len() == 0
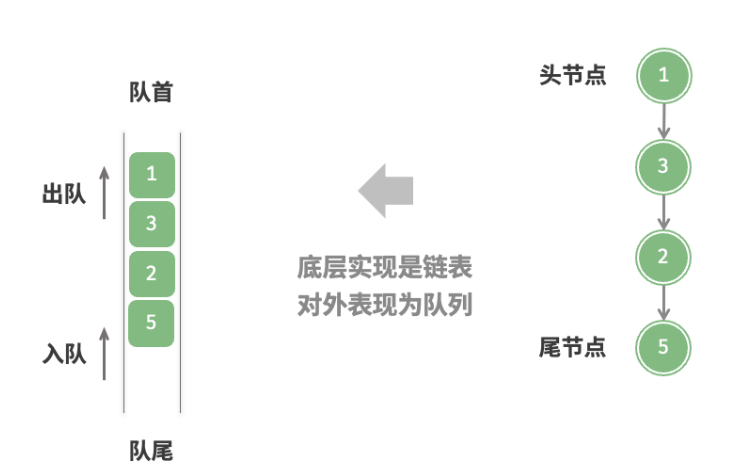
队列实现 基于链表的实现 如下图所示,我们可以将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”,规定队尾仅可添加节点,队首仅可删除节点。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 class LinkedListQueue : """基于链表实现的队列""" def __init__ (self ): """构造方法""" self.__front: ListNode | None = None self.__rear: ListNode | None = None self.__size: int = 0 def size (self ) -> int : """获取队列的长度""" return self.__size def is_empty (self ) -> bool : """判断队列是否为空""" return not self.__front def push (self, num: int ): """入队""" node = ListNode(num) if self.__front is None : self.__front = node self.__rear = node else : self.__rear.next = node self.__rear = node self.__size += 1 def pop (self ) -> int : """出队""" num = self.peek() self.__front = self.__front.next self.__size -= 1 return num def peek (self ) -> int : """访问队首元素""" if self.size() == 0 : print ("队列为空" ) return False return self.__front.val def to_list (self ) -> list [int ]: """转化为列表用于打印""" queue = [] temp = self.__front while temp: queue.append(temp.val) temp = temp.next return queue
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 type linkedListQueue struct { data *list.List } func newLinkedListQueue () return &linkedListQueue{ data: list.New(), } } func (s *linkedListQueue) s.data.PushBack(value) } func (s *linkedListQueue) if s.isEmpty() { return nil } e := s.data.Front() s.data.Remove(e) return e.Value } func (s *linkedListQueue) if s.isEmpty() { return nil } e := s.data.Front() return e.Value } func (s *linkedListQueue) int { return s.data.Len() } func (s *linkedListQueue) bool { return s.data.Len() == 0 } func (s *linkedListQueue) return s.data }
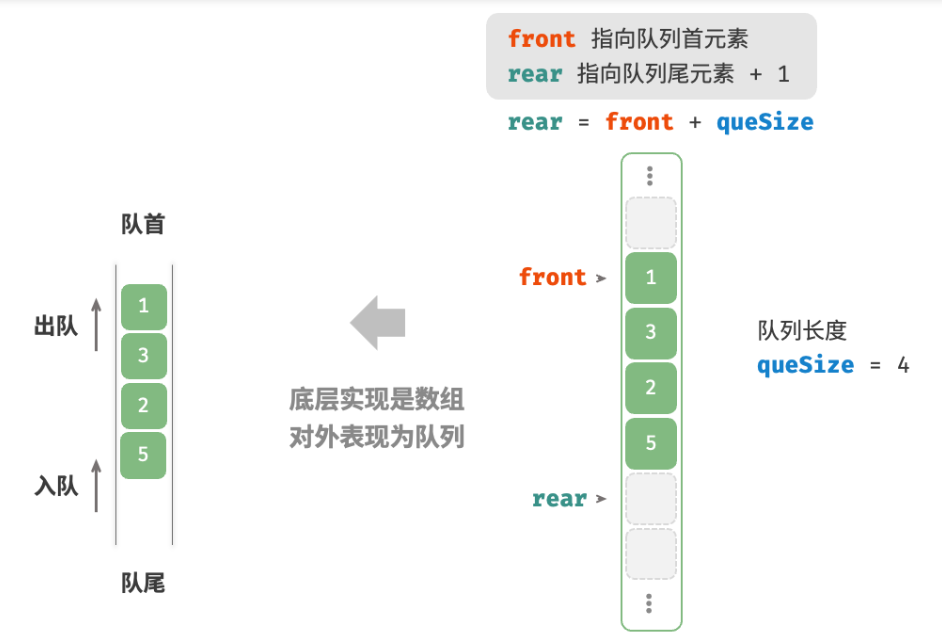
基于数组的实现 由于数组删除首元素的时间复杂度为O(n),这会导致出队操作效率较低。然而,我们可以采用以下巧妙方法来避免这个问题。
我们可以使用一个变量 front 指向队首元素的索引,并维护一个变量 size 用于记录队列长度。定义 rear = front + size ,这个公式计算出的 rear 指向队尾元素之后的下一个位置。
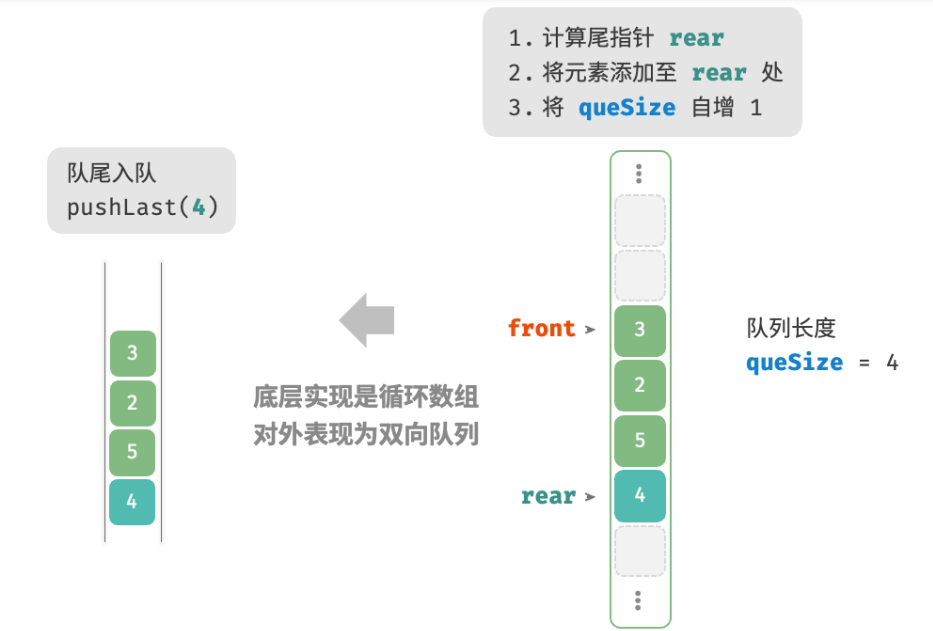
基于此设计,**数组中包含元素的有效区间为 [front, rear - 1]**,各种操作的实现方法如下图所示。
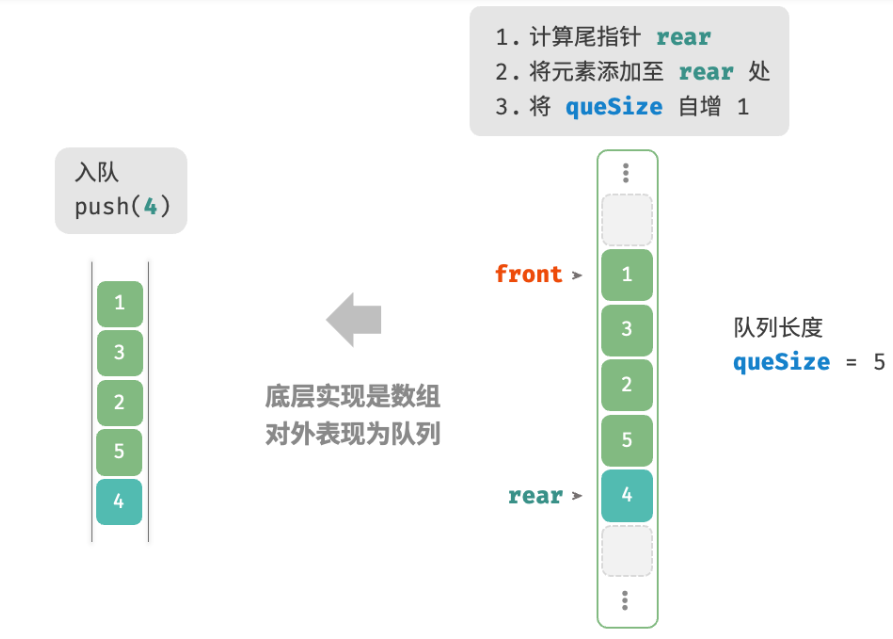
入队操作:将输入元素赋值给 rear 索引处,并将 size 增加 1 。
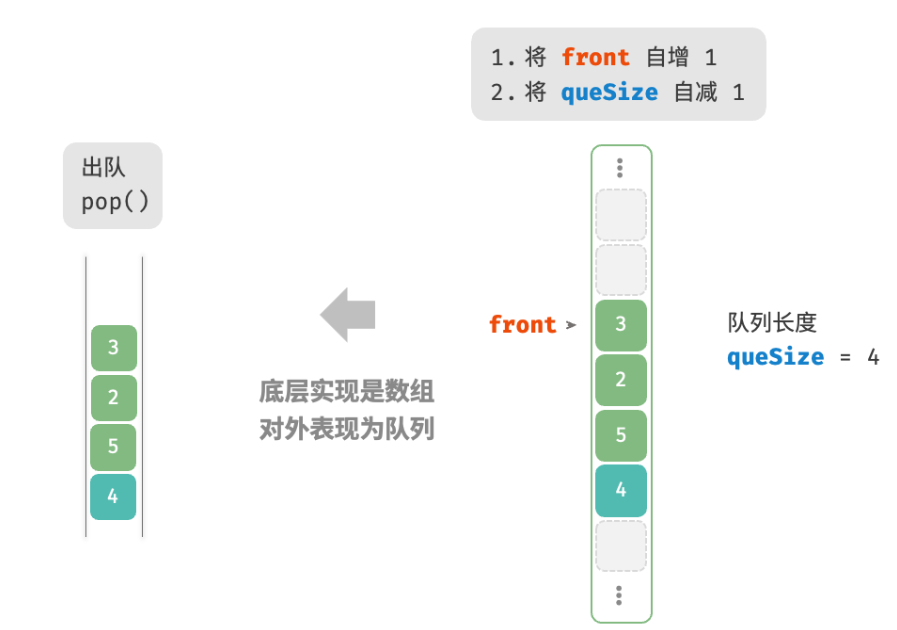
出队操作:只需将 front 增加 1 ,并将 size 减少 1 。
可以看到,入队和出队操作都只需进行一次操作,时间复杂度均为 O(1) 。
你可能会发现一个问题:在不断进行入队和出队的过程中,front 和 rear 都在向右移动,当它们到达数组尾部时就无法继续移动了 。为解决此问题,我们可以将数组视为首尾相接的“环形数组”。
对于环形数组,我们需要让 front 或 rear 在越过数组尾部时,直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现,代码如下所示。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 class ArrayQueue : """基于环形数组实现的队列""" def __init__ (self, size: int ): """构造方法""" self.__nums: list [int ] = [0 ] * size self.__front: int = 0 self.__size: int = 0 def capacity (self ) -> int : """获取队列的容量""" return len (self.__nums) def size (self ) -> int : """获取队列的长度""" return self.__size def is_empty (self ) -> bool : """判断队列是否为空""" return self.__size == 0 def push (self, num: int ): """入队""" if self.__size == self.capacity(): raise IndexError("队列已满" ) rear: int = (self.__front + self.__size) % self.capacity() self.__nums[rear] = num self.__size += 1 def pop (self ) -> int : """出队""" num: int = self.peek() self.__front = (self.__front + 1 ) % self.capacity() self.__size -= 1 return num def peek (self ) -> int : """访问队首元素""" if self.is_empty(): raise IndexError("队列为空" ) return self.__nums[self.__front] def to_list (self ) -> list [int ]: """返回列表用于打印""" res = [0 ] * self.size() j: int = self.__front for i in range (self.size()): res[i] = self.__nums[(j % self.capacity())] j += 1 return res
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 type arrayQueue struct { nums []int front int queSize int queCapacity int } func newArrayQueue (queCapacity int ) return &arrayQueue{ nums: make ([]int , queCapacity), queCapacity: queCapacity, front: 0 , queSize: 0 , } } func (q *arrayQueue) int { return q.queSize } func (q *arrayQueue) bool { return q.queSize == 0 } func (q *arrayQueue) int ) { if q.queSize == q.queCapacity { return } rear := (q.front + q.queSize) % q.queCapacity q.nums[rear] = num q.queSize++ } func (q *arrayQueue) num := q.peek() q.front = (q.front + 1 ) % q.queCapacity q.queSize-- return num } func (q *arrayQueue) if q.isEmpty() { return nil } return q.nums[q.front] } func (q *arrayQueue) int { rear := (q.front + q.queSize) if rear >= q.queCapacity { rear %= q.queCapacity return append (q.nums[q.front:], q.nums[:rear]...) } return q.nums[q.front:rear] }
以上实现的队列仍然具有局限性,即其长度不可变。然而,这个问题不难解决,我们可以将数组替换为动态数组,从而引入扩容机制。
两种实现的对比结论与栈一致。
队列典型应用
淘宝订单 。购物者下单后,订单将加入队列中,系统随后会根据顺序依次处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发成为工程师们需要重点攻克的问题。各类待办事项 。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等。队列在这些场景中可以有效地维护处理顺序。
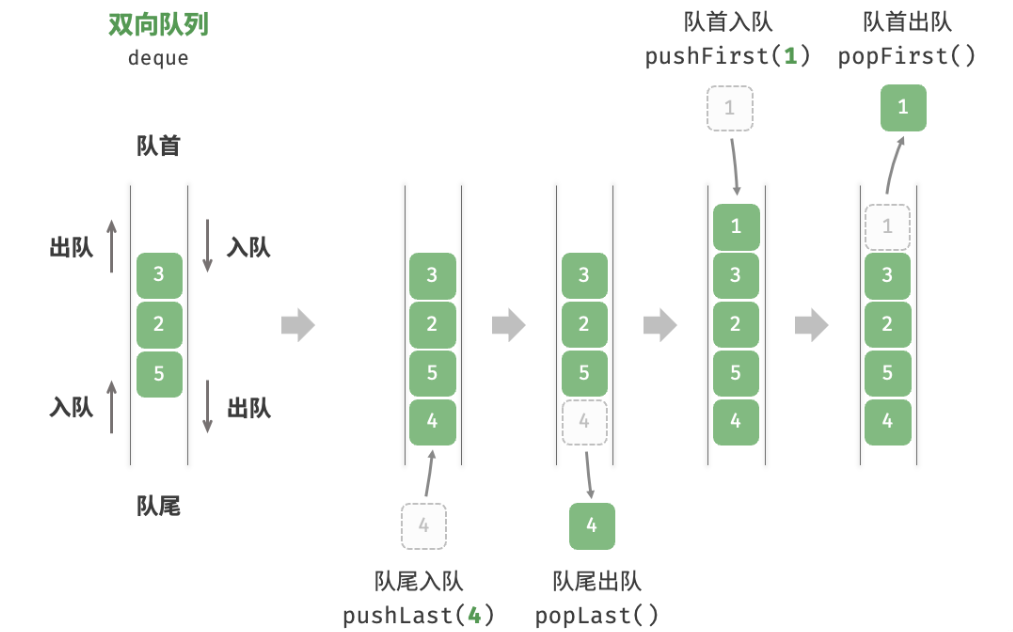
双向队列 在队列中,我们仅能在头部删除或在尾部添加元素。双向队列提供了更高的灵活性,允许在头部和尾部执行元素的添加或删除操作。
双向队列常用操作 双向队列的常用操作如下表所示,具体的方法名称需要根据所使用的编程语言来确定。
表 双向队列操作效率
方法名
描述
时间复杂度
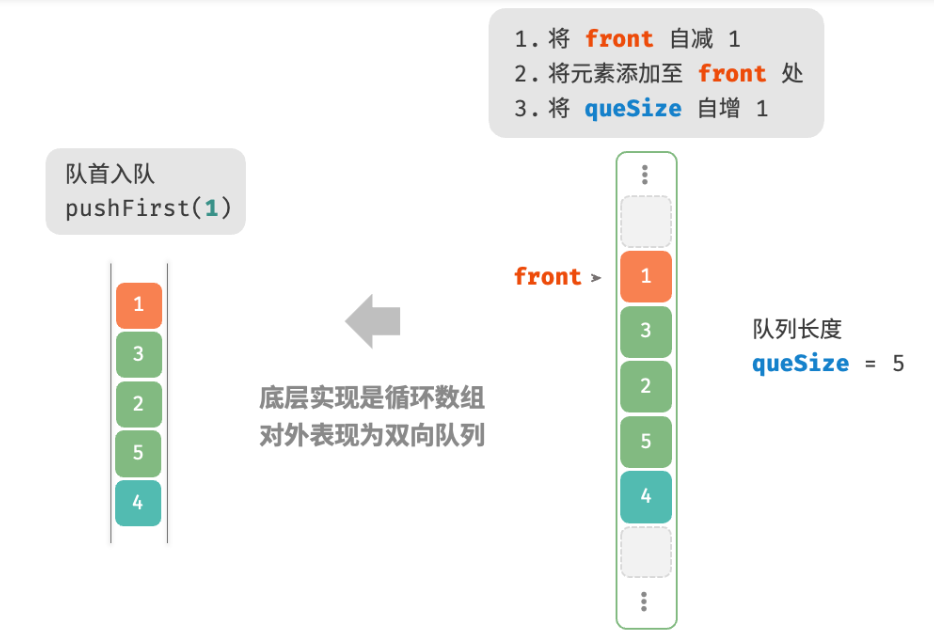
pushFirst()
将元素添加至队首
O(1)
pushLast()
将元素添加至队尾
O(1)
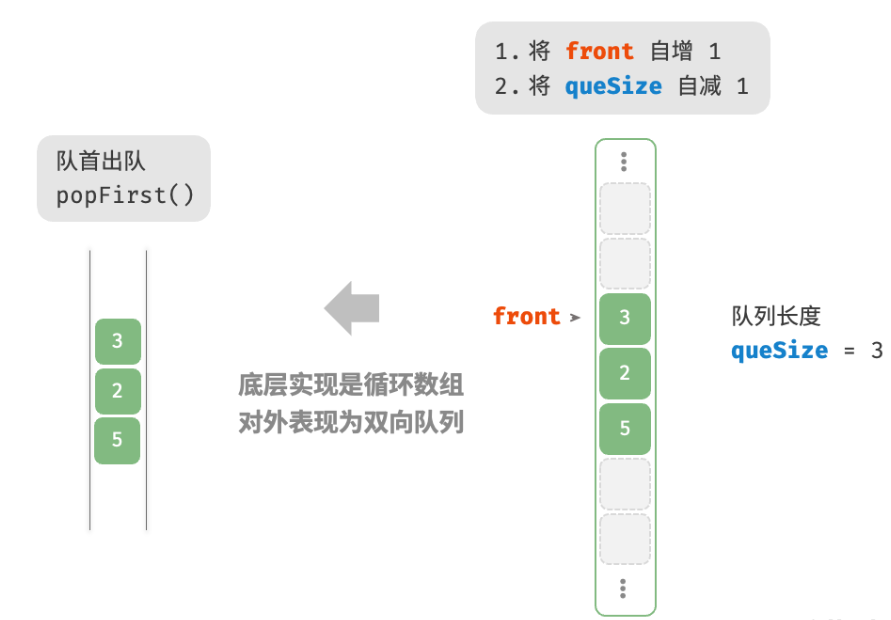
popFirst()
删除队首元素
O(1)
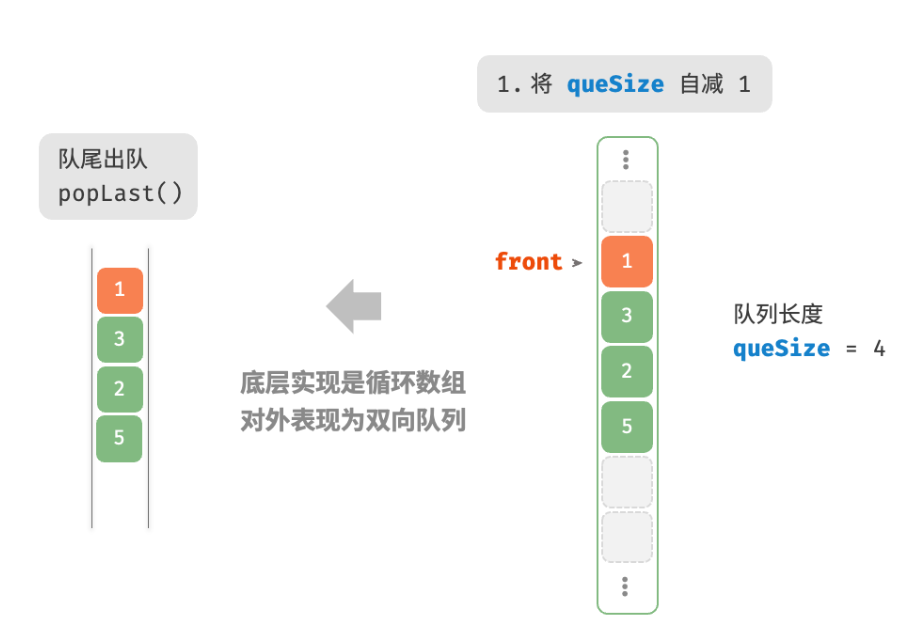
popLast()
删除队尾元素
O(1)
peekFirst()
访问队首元素
O(1)
peekLast()
访问队尾元素
O(1)
我们可以直接使用编程语言中已实现的双向队列类。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 deque: deque[int ] = collections.deque() deque.append(2 ) deque.append(5 ) deque.append(4 ) deque.appendleft(3 ) deque.appendleft(1 ) front: int = deque[0 ] rear: int = deque[-1 ] pop_front: int = deque.popleft() pop_rear: int = deque.pop() size: int = len (deque) is_empty: bool = len (deque) == 0
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 deque := list.New() deque.PushBack(2 ) deque.PushBack(5 ) deque.PushBack(4 ) deque.PushFront(3 ) deque.PushFront(1 ) front := deque.Front() rear := deque.Back() deque.Remove(front) deque.Remove(rear) size := deque.Len() isEmpty := deque.Len() == 0
双向队列实现 双向队列的实现与队列类似,可以选择链表或数组作为底层数据结构。
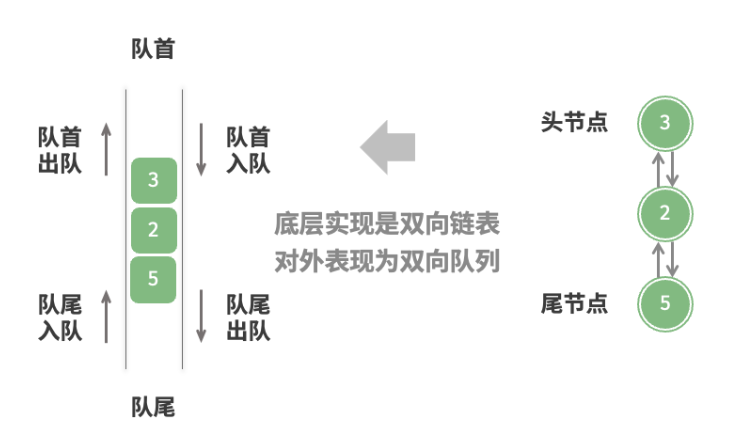
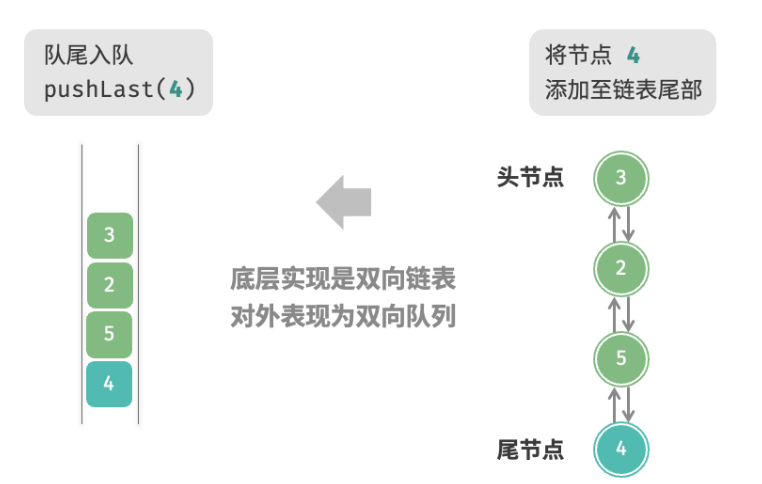
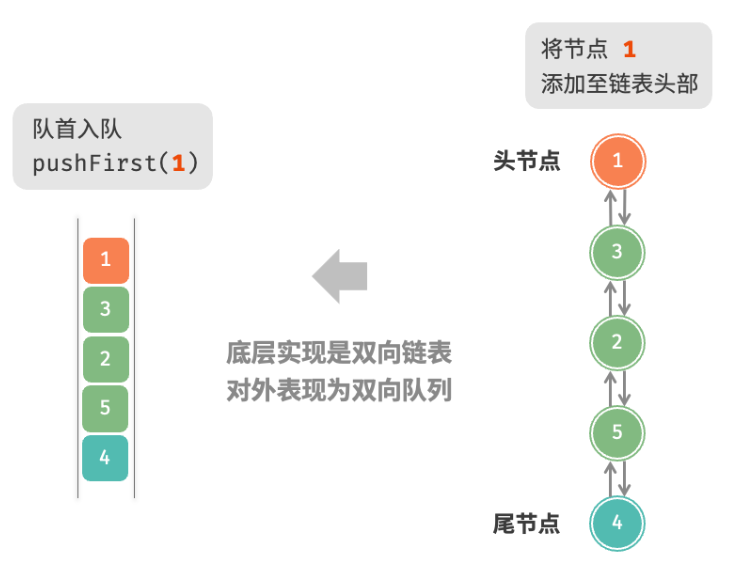
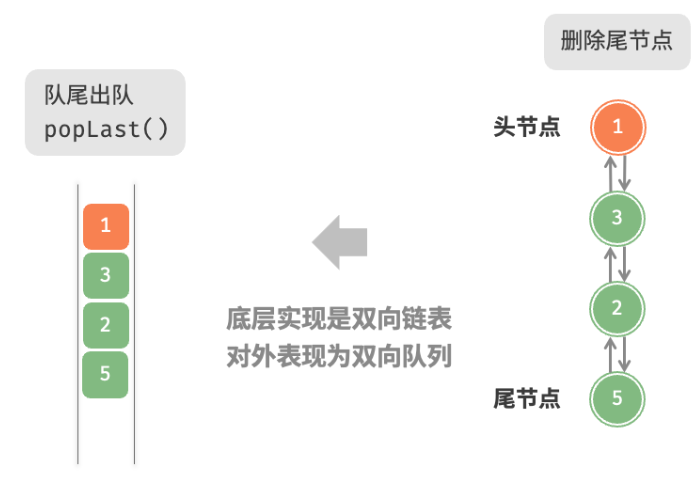
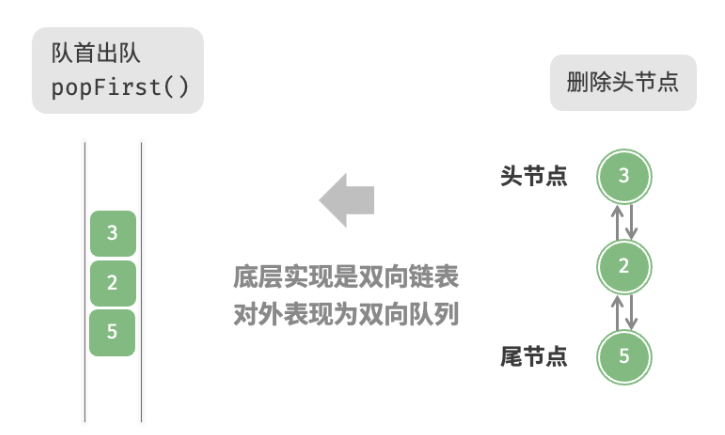
基于双向链表的实现 采用“双向链表”作为双向队列的底层数据结构。如下图所示,我们将双向链表的头节点和尾节点视为双向队列的队首和队尾,同时实现在两端添加和删除节点的功能。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 class ListNode : """双向链表节点""" def __init__ (self, val: int ): """构造方法""" self.val: int = val self.next : ListNode | None = None self.prev: ListNode | None = None class LinkedListDeque : """基于双向链表实现的双向队列""" def __init__ (self ): """构造方法""" self.front: ListNode | None = None self.rear: ListNode | None = None self.__size: int = 0 def size (self ) -> int : """获取双向队列的长度""" return self.__size def is_empty (self ) -> bool : """判断双向队列是否为空""" return self.size() == 0 def push (self, num: int , is_front: bool ): """入队操作""" node = ListNode(num) if self.is_empty(): self.front = self.rear = node elif is_front: self.front.prev = node node.next = self.front self.front = node else : self.rear.next = node node.prev = self.rear self.rear = node self.__size += 1 def push_first (self, num: int ): """队首入队""" self.push(num, True ) def push_last (self, num: int ): """队尾入队""" self.push(num, False ) def pop (self, is_front: bool ) -> int : """出队操作""" if self.is_empty(): return None if is_front: val: int = self.front.val fnext: ListNode | None = self.front.next if fnext != None : fnext.prev = None self.front.next = None self.front = fnext else : val: int = self.rear.val rprev: ListNode | None = self.rear.prev if rprev != None : rprev.next = None self.rear.prev = None self.rear = rprev self.__size -= 1 return val def pop_first (self ) -> int : """队首出队""" return self.pop(True ) def pop_last (self ) -> int : """队尾出队""" return self.pop(False ) def peek_first (self ) -> int : """访问队首元素""" return None if self.is_empty() else self.front.val def peek_last (self ) -> int : """访问队尾元素""" return None if self.is_empty() else self.rear.val def to_array (self ) -> list [int ]: """返回数组用于打印""" node = self.front res = [0 ] * self.size() for i in range (self.size()): res[i] = node.val node = node.next return res
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 type linkedListDeque struct { data *list.List } func newLinkedListDeque () return &linkedListDeque{ data: list.New(), } } func (s *linkedListDeque) s.data.PushFront(value) } func (s *linkedListDeque) s.data.PushBack(value) } func (s *linkedListDeque) if s.isEmpty() { return nil } e := s.data.Front() s.data.Remove(e) return e.Value } func (s *linkedListDeque) if s.isEmpty() { return nil } e := s.data.Back() s.data.Remove(e) return e.Value } func (s *linkedListDeque) if s.isEmpty() { return nil } e := s.data.Front() return e.Value } func (s *linkedListDeque) if s.isEmpty() { return nil } e := s.data.Back() return e.Value } func (s *linkedListDeque) int { return s.data.Len() } func (s *linkedListDeque) bool { return s.data.Len() == 0 } func (s *linkedListDeque) return s.data }
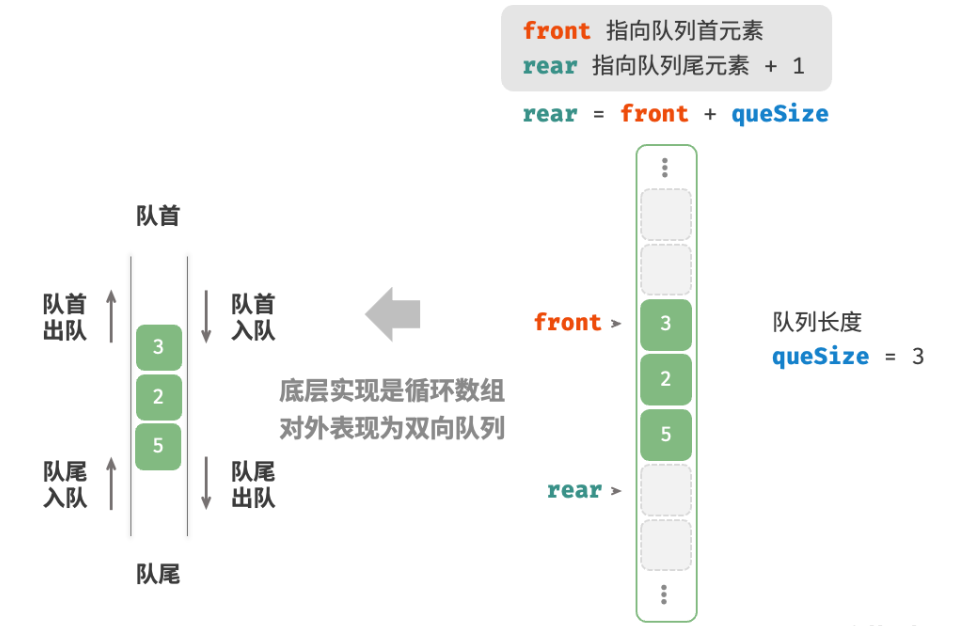
基于数组的实现 如下图所示,与基于数组实现队列类似,我们也可以使用环形数组来实现双向队列。
在队列的实现基础上,仅需增加“队首入队”和“队尾出队”的方法。
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 class ArrayDeque : """基于环形数组实现的双向队列""" def __init__ (self, capacity: int ): """构造方法""" self.__nums: list [int ] = [0 ] * capacity self.__front: int = 0 self.__size: int = 0 def capacity (self ) -> int : """获取双向队列的容量""" return len (self.__nums) def size (self ) -> int : """获取双向队列的长度""" return self.__size def is_empty (self ) -> bool : """判断双向队列是否为空""" return self.__size == 0 def index (self, i: int ) -> int : """计算环形数组索引""" return (i + self.capacity()) % self.capacity() def push_first (self, num: int ): """队首入队""" if self.__size == self.capacity(): print ("双向队列已满" ) return self.__front = self.index(self.__front - 1 ) self.__nums[self.__front] = num self.__size += 1 def push_last (self, num: int ): """队尾入队""" if self.__size == self.capacity(): print ("双向队列已满" ) return rear = self.index(self.__front + self.__size) self.__nums[rear] = num self.__size += 1 def pop_first (self ) -> int : """队首出队""" num = self.peek_first() self.__front = self.index(self.__front + 1 ) self.__size -= 1 return num def pop_last (self ) -> int : """队尾出队""" num = self.peek_last() self.__size -= 1 return num def peek_first (self ) -> int : """访问队首元素""" if self.is_empty(): raise IndexError("双向队列为空" ) return self.__nums[self.__front] def peek_last (self ) -> int : """访问队尾元素""" if self.is_empty(): raise IndexError("双向队列为空" ) last = self.index(self.__front + self.__size - 1 ) return self.__nums[last] def to_array (self ) -> list [int ]: """返回数组用于打印""" res = [] for i in range (self.__size): res.append(self.__nums[self.index(self.__front + i)]) return res
Go:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 type arrayDeque struct { nums []int front int queSize int queCapacity int } func newArrayDeque (queCapacity int ) return &arrayDeque{ nums: make ([]int , queCapacity), queCapacity: queCapacity, front: 0 , queSize: 0 , } } func (q *arrayDeque) int { return q.queSize } func (q *arrayDeque) bool { return q.queSize == 0 } func (q *arrayDeque) int ) int { return (i + q.queCapacity) % q.queCapacity } func (q *arrayDeque) int ) { if q.queSize == q.queCapacity { fmt.Println("双向队列已满" ) return } q.front = q.index(q.front - 1 ) q.nums[q.front] = num q.queSize++ } func (q *arrayDeque) int ) { if q.queSize == q.queCapacity { fmt.Println("双向队列已满" ) return } rear := q.index(q.front + q.queSize) q.nums[rear] = num q.queSize++ } func (q *arrayDeque) num := q.peekFirst() q.front = q.index(q.front + 1 ) q.queSize-- return num } func (q *arrayDeque) num := q.peekLast() q.queSize-- return num } func (q *arrayDeque) if q.isEmpty() { return nil } return q.nums[q.front] } func (q *arrayDeque) if q.isEmpty() { return nil } last := q.index(q.front + q.queSize - 1 ) return q.nums[last] } func (q *arrayDeque) int { res := make ([]int , q.queSize) for i, j := 0 , q.front; i < q.queSize; i++ { res[i] = q.nums[q.index(j)] j++ } return res }
双向队列应用 双向队列兼具栈与队列的逻辑,因此它可以实现这两者的所有应用场景,同时提供更高的自由度 。
我们知道,软件的“撤销”功能通常使用栈来实现:系统将每次更改操作 push 到栈中,然后通过 pop 实现撤销。然而,考虑到系统资源的限制,软件通常会限制撤销的步数(例如仅允许保存50步)。当栈的长度超过50时,软件需要在栈底(即队首)执行删除操作。但栈无法实现该功能,此时就需要使用双向队列来替代栈 。请注意,“撤销”的核心逻辑仍然遵循栈的先入后出原则,只是双向队列能够更加灵活地实现一些额外逻辑。
References:https://www.hello-algo.com/chapter_stack_and_queue/