加载中...

leetcode二叉树必刷题（2）——N 叉树的层序遍历、在每个树行中找最大值、填充每个节点的下一个右侧节点指针、填充每个节点的下一个右侧节点指针II、二叉树的最大深度、二叉树的最小深度

发表于2023-11-28|更新于2023-12-02

|字数总计:4.1k|阅读时长:21分钟|阅读量:

N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

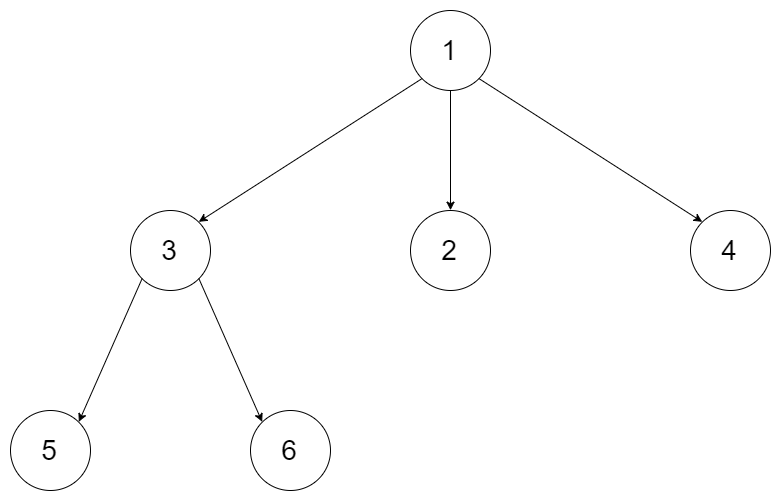
1 2	输入：root = [1,null,3,2,4,null,5,6] 输出：[[1],[3,2,4],[5,6]]

示例 2：

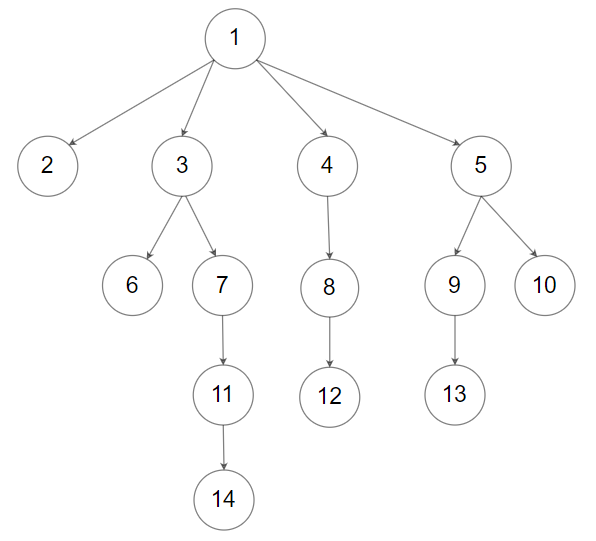
1 2	输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

树的高度不会超过 1000
树的节点总数在 [0, 10^4] 之间

Python：

#BFS
"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution:
    def levelOrder(self, root: 'Node') -> List[List[int]]:
        if not root:
            return []

        out = []
        q = deque([root])

        while q:
            level_values = []
            level_size = len(q)

            for _ in range(level_size):
                node = q.popleft()
                level_values.append(node.val)
                q.extend(node.children)

            out.append(level_values)

        return out

#DFS
"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution:
    def levelOrder(self, root: 'Node') -> List[List[int]]:
        out = []
        def dfs(node, depth):
            if not node:
                return

            if depth == len(out):
                out.append([])

            out[depth].append(node.val)

            for child in node.children:
                dfs(child, depth + 1)

        dfs(root, 0)
        return out

Go：

//BFS
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func levelOrder(root *Node) (out [][]int) {
	if root == nil {
		return
	}
	q := []*Node{root}
	for len(q) > 0 {
		var tmp []int
		l := len(q)
		for i := 0; i < l; i++ {
			node := q[i]
			tmp = append(tmp, node.Val)
			for _, v := range node.Children {
				q = append(q, v)
			}
		}
		q = q[l:]
		out = append(out, tmp)
	}
	return
}

//DFS
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func levelOrder(root *Node) (out [][]int) {
	var dfs func(*Node, int)
	dfs = func(node *Node, depth int) {
		if node == nil {
			return
		}
		if depth == len(out) {
			out = append(out, []int{})
		}
		out[depth] = append(out[depth], node.Val)
		for _, v := range node.Children {
			dfs(v, depth+1)
		}
	}
	dfs(root, 0)
	return
}

//BFS
func levelOrder(root *Node) (ans [][]int) {
    if root == nil {
        return
    }
    q := []*Node{root}
    for q != nil {
        level := []int{}
        tmp := q
        q = nil
        for _, node := range tmp {
            level = append(level, node.Val)
            q = append(q, node.Children...)
        }
        ans = append(ans, level)
    }
    return
}

在每个树行中找最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

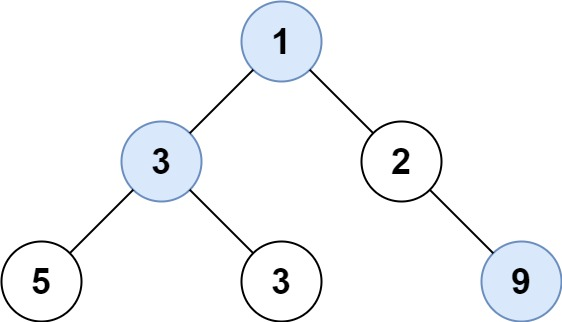
1 2	输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9]

示例2：

1 2	输入: root = [1,2,3] 输出: [1,3]

提示：

二叉树的节点个数的范围是 [0,104]
-2^31 <= Node.val <= 2^31 - 1

Python：

# BFS
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []

        out = []
        q = [root]

        while q:
            tmp = q.copy()
            maximum = tmp[0].val
            q = []

            for node in tmp:
                if node.val > maximum:
                    maximum = node.val

                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)

            out.append(maximum)

        return out

# DFS
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        def dfs(node, depth):
            if not node:
                return

            if depth == len(out):
                out.append(node.val)
            else:
                if node.val > out[depth]:
                    out[depth] = node.val

            dfs(node.left, depth + 1)
            dfs(node.right, depth + 1)

        out = []
        dfs(root, 0)
        return out

Go：

//BFS
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func largestValues(root *TreeNode) (out []int) {
	if root == nil {
		return nil
	}
	q := []*TreeNode{root}
	for len(q) > 0 {
		tmp := q
		max := tmp[0].Val
		q = nil
		for _, node := range tmp {
			if node.Val > max {
				max = node.Val
			}
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}
		out = append(out, max)
	}
	return
}

//DFS
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func largestValues(root *TreeNode) (out []int) {
	var dfs func(*TreeNode, int)
	dfs = func(node *TreeNode, depth int) {
		if node == nil {
			return
		}
		if depth == len(out) {
			out = append(out, node.Val)
		} else {
			if node.Val > out[depth] {
				out[depth] = node.Val
			}
		}
		dfs(node.Left, depth+1)
		dfs(node.Right, depth+1)
	}
	dfs(root, 0)
	return
}

填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

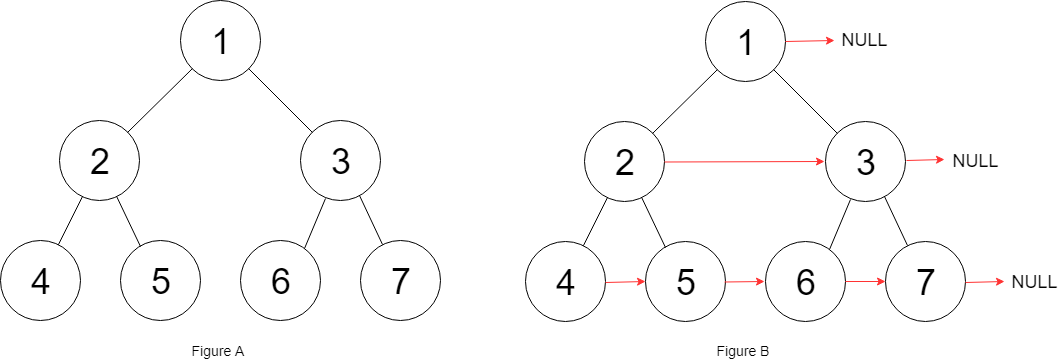
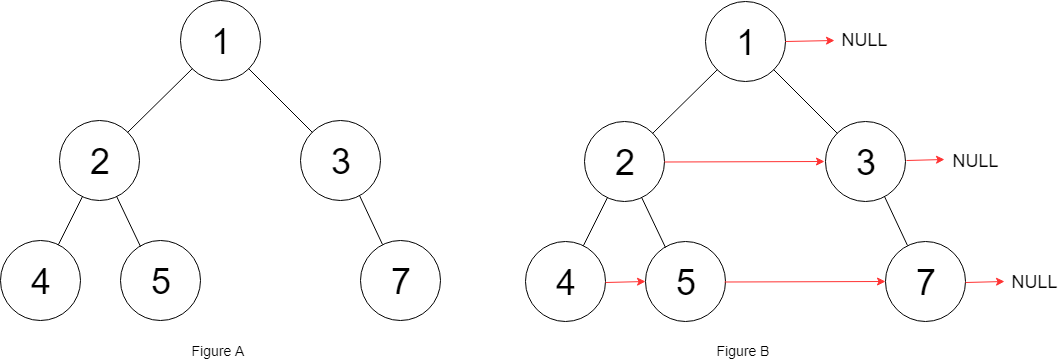
1
2
3

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

1 2	输入：root = [] 输出：[]

提示：

树中节点的数量在 [0, 212 - 1] 范围内
-1000 <= node.val <= 1000

Python：

#官方解法
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        
        if not root:
            return root
        
        # 从根节点开始
        leftmost = root
        
        while leftmost.left:
            
            # 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
            head = leftmost
            while head:
                
                # CONNECTION 1
                head.left.next = head.right
                
                # CONNECTION 2
                if head.next:
                    head.right.next = head.next.left
                
                # 指针向后移动
                head = head.next
            
            # 去下一层的最左的节点
            leftmost = leftmost.left
        
        return root

#官方解法，BFS
import collections 

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        
        if not root:
            return root
        
        # 初始化队列同时将第一层节点加入队列中，即根节点
        Q = collections.deque([root])
        
        # 外层的 while 循环迭代的是层数
        while Q:
            
            # 记录当前队列大小
            size = len(Q)
            
            # 遍历这一层的所有节点
            for i in range(size):
                
                # 从队首取出元素
                node = Q.popleft()
                
                # 连接
                if i < size - 1:
                    node.next = Q[0]
                
                # 拓展下一层节点
                if node.left:
                    Q.append(node.left)
                if node.right:
                    Q.append(node.right)
        
        # 返回根节点
        return root

#BFS,本人解法
class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if root is None:
            return root
    
        q = [root]
        
        def insert(arr, node):
            l = len(arr)
            if l != 0:
                arr[-1].next = node
                arr.append(node)
                return arr
            arr.append(node)
            return arr
        
        while len(q) > 0:
            tmp = q
            q = []
            for node in tmp:
                if node.left:
                    q = insert(q, node.left)
                    q = insert(q, node.right)
        
        return root

#DFS，本人解法
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        
        arr = []

        def dfs(node, level):
            nonlocal arr
            if node is None:
                return

            if level == len(arr):
                arr.append([])

            if len(arr[level]) > 0:
                arr[level][-1].next = node

            arr[level].append(node)

            dfs(node.left, level + 1)
            dfs(node.right, level + 1)

        dfs(root, 0)
        return root

Go：

//官方解法
func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    // 每次循环从该层的最左侧节点开始
    for leftmost := root; leftmost.Left != nil; leftmost = leftmost.Left {
        // 通过 Next 遍历这一层节点，为下一层的节点更新 Next 指针
        for node := leftmost; node != nil; node = node.Next {
            // 左节点指向右节点
            node.Left.Next = node.Right
 
            // 右节点指向下一个左节点
            if node.Next != nil {
                node.Right.Next = node.Next.Left
            }
        }
    }

    // 返回根节点
    return root
}

//BFS，官方解法
func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    // 初始化队列同时将第一层节点加入队列中，即根节点
    queue := []*Node{root}

    // 循环迭代的是层数
    for len(queue) > 0 {
        tmp := queue
        queue = nil

        // 遍历这一层的所有节点
        for i, node := range tmp {
            // 连接
            if i+1 < len(tmp) {
                node.Next = tmp[i+1]
            }

            // 拓展下一层节点
            if node.Left != nil {
                queue = append(queue, node.Left)
                queue = append(queue, node.Right)
            }
        }
    }

    // 返回根节点
    return root
}

//BFS,本人解法
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
	if root == nil {
		return root
	}
	q := []*Node{root}
	insert := func(arr []*Node, node *Node) []*Node {
		l := len(arr)
		if l != 0 {
			arr[l-1].Next = node
			arr = append(arr, node)
			return arr
		}
		// node.Next = nil
		arr = append(arr, node)
		return arr
	}
	for len(q) > 0 {
		tmp := q
		q = nil
		for _, node := range tmp {
			if node.Left != nil {
				q = insert(q, node.Left)
				q = insert(q, node.Right)
			}
		}
	}
	return root
}

//DFS，本人解法
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
	var arr [][]*Node

	var dfs func(*Node, int)
	dfs = func(node *Node, level int) {
		if node == nil {
			return
		}

		if level == len(arr) {
			arr = append(arr, []*Node{})
		}

		if len(arr[level]) > 0 {
			arr[level][len(arr[level])-1].Next = node
		}

		arr[level] = append(arr[level], node)

		dfs(node.Left, level+1)
		dfs(node.Right, level+1)
	}

	dfs(root, 0)
	return root
}

填充每个节点的下一个右侧节点指针 II

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

1
2
3

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

1 2	输入：root = [] 输出：[]

提示：

树中的节点数在范围 [0, 6000] 内
-100 <= Node.val <= 100

Python：

#BFS
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        
        if not root:
            return root
        
        # 初始化队列同时将第一层节点加入队列中，即根节点
        Q = collections.deque([root])
        
        # 外层的 while 循环迭代的是层数
        while Q:
            
            # 记录当前队列大小
            size = len(Q)
            
            # 遍历这一层的所有节点
            for i in range(size):
                
                # 从队首取出元素
                node = Q.popleft()
                
                # 连接
                if i < size - 1:
                    node.next = Q[0]
                
                # 拓展下一层节点
                if node.left:
                    Q.append(node.left)
                if node.right:
                    Q.append(node.right)
        
        # 返回根节点
        return root

#BFS，与上题类似
class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if root is None:
            return root
    
        q = [root]
        
        def insert(arr, node):
            l = len(arr)
            if l != 0:
                arr[-1].next = node
                arr.append(node)
                return arr
            arr.append(node)
            return arr
        
        while len(q) > 0:
            tmp = q
            q = []
            for node in tmp:
                if node.left:
                    q = insert(q, node.left)
                if node.right:
                    q = insert(q, node.right)
        
        return root

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
#DFS，与上题类似
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        
        arr = []

        def dfs(node, level):
            nonlocal arr
            if node is None:
                return

            if level == len(arr):
                arr.append([])

            if len(arr[level]) > 0:
                arr[level][-1].next = node

            arr[level].append(node)

            dfs(node.left, level + 1)
            dfs(node.right, level + 1)

        dfs(root, 0)
        return root

Go：

//跟上题解法类似，BFS
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
	if root == nil {
		return root
	}

	// 初始化队列同时将第一层节点加入队列中，即根节点
	queue := []*Node{root}

	// 循环迭代的是层数
	for len(queue) > 0 {
		tmp := queue
		queue = nil

		// 遍历这一层的所有节点
		for i, node := range tmp {
			// 连接
			if i+1 < len(tmp) {
				node.Next = tmp[i+1]
			}
			// 拓展下一层节点
			if node.Left != nil {
				queue = append(queue, node.Left)
			}
			if node.Right != nil {
				queue = append(queue, node.Right)
			}
		}
	}

	// 返回根节点
	return root
}

//BFS
func connect(root *Node) *Node {
	if root == nil {
		return root
	}
	q := []*Node{root}
	insert := func(arr []*Node, node *Node) []*Node {
		l := len(arr)
		if l != 0 {
			arr[l-1].Next = node
			arr = append(arr, node)
			return arr
		}
		// node.Next = nil
		arr = append(arr, node)
		return arr
	}
	for len(q) > 0 {
		tmp := q
		q = nil
		for _, node := range tmp {
			if node.Left != nil {
				q = insert(q, node.Left)
			}
			if node.Right != nil {
				q = insert(q, node.Right)
			}
		}
	}
	return root
}

//与上题类似，DFS同样适用
func connect(root *Node) *Node {
	var arr [][]*Node

	var dfs func(*Node, int)
	dfs = func(node *Node, level int) {
		if node == nil {
			return
		}

		if level == len(arr) {
			arr = append(arr, []*Node{})
		}

		if len(arr[level]) > 0 {
			arr[level][len(arr[level])-1].Next = node
		}

		arr[level] = append(arr[level], node)

		dfs(node.Left, level+1)
		dfs(node.Right, level+1)
	}

	dfs(root, 0)
	return root
}

二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

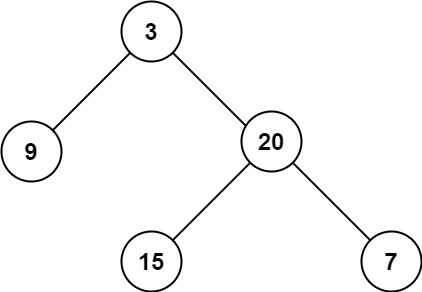
1 2	输入：root = [3,9,20,null,null,15,7] 输出：3

示例 2：

1 2	输入：root = [1,null,2] 输出：2

提示：

树中节点的数量在 [0, 10^4] 区间内。
-100 <= Node.val <= 100

Python：

#官方解法，DFS
class Solution:
    def maxDepth(self, root):
        if root is None: 
            return 0 
        else: 
            left_height = self.maxDepth(root.left) 
            right_height = self.maxDepth(root.right) 
            return max(left_height, right_height) + 1

#本人解法，BFS
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        max_depth = 0
        queue = collections.deque([root])

        while queue:
            size = len(queue)
            for _ in range(size):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            max_depth += 1

        return max_depth

##本人解法，DFS
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        def dfs(node: TreeNode, depth: int) -> None:
            nonlocal max_depth
            if not node:
                return
            if depth > max_depth:
                max_depth = depth
            dfs(node.left, depth + 1)
            dfs(node.right, depth + 1)

        max_depth = 0
        dfs(root, 1)
        return max_depth

Go：

//官方解法，DFS
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

//DFS，本人解法
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
	var dfs func(*TreeNode, int)
	max := 0
	dfs = func(node *TreeNode, depth int) {
		if node == nil {
			return
		}
		if depth > max {
			max = depth
		}
		dfs(node.Left, depth+1)
		dfs(node.Right, depth+1)
	}
	dfs(root, 1)
	return max
}

//本人解法，BFS
func maxDepth(root *TreeNode) (max int) {
	if root == nil {
		return
	}
	q := []*TreeNode{root}
	for len(q) > 0 {
		tmp := q
		q = nil
		for _, node := range tmp {
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}
		max++
	}
	return
}

二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

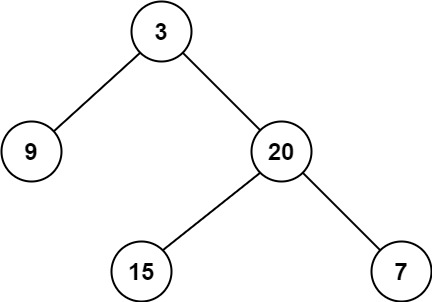
1 2	输入：root = [3,9,20,null,null,15,7] 输出：2

示例 2：

1 2	输入：root = [2,null,3,null,4,null,5,null,6] 输出：5

提示：

树中节点数的范围在 [0, 10^5] 内
-1000 <= Node.val <= 1000

Python：

#DFS
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        def dfs(node, depth):
            if node is None:
                return depth - 1
            if node.left is None and node.right is None:
                return depth
            left = dfs(node.left, depth + 1)
            right = dfs(node.right, depth + 1)
            if node.left is None:
                return right
            if node.right is None:
                return left
            return min(left, right)

        return dfs(root, 1)

# 本人解法，BFS
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        min_depth = 0
        queue = deque([root])

        while queue:
            size = len(queue)
            min_depth += 1

            for _ in range(size):
                node = queue.popleft()

                if not node.left and not node.right:
                    return min_depth

                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

        return min_depth

Go：

//本人解法，BFS
func minDepth(root *TreeNode) (min int) {
	if root == nil {
		return 0
	}
	q := []*TreeNode{root}
	for len(q) > 0 {
		tmp := q
		q = nil
		min++
		for _, node := range tmp {
			if node.Left == nil && node.Right == nil {
				return
			}
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}
	}
	return
}

//本人解法，DFS
func minDepth(root *TreeNode) int {
	var dfs func(*TreeNode, int) int
	dfs = func(node *TreeNode, depth int) int {
		if node == nil {
			return depth - 1
		}

		if node.Left == nil && node.Right == nil {
			return depth
		}
		left := dfs(node.Left, depth+1)
		right := dfs(node.Right, depth+1)
		if node.Left == nil {
			return right
		}
		if node.Right == nil {
			return left
		}
		return min(left, right)
	}
	return dfs(root, 1)
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

//注意，考虑一个只有左子节点的节点。在这种情况下，node.Left != nil 和 node.Right == nil。如果我们删除了这两行代码，那么函数将返回 min(left, right)，即 min(depth of left subtree, 0)，结果将是0，这是不正确的。正确的行为是返回右子树（即左子树）的深度，因为这是唯一存在的子树。因此，这两行代码确保了函数在处理只有一个子节点的节点时的正确行为。如果删除它们，函数将无法正确处理这种情况。

文章作者: 王翊珩

文章链接: https://palp1tate.github.io/2023/11/28/%E7%AE%97%E6%B3%95/q8/

版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自王翊珩！

大三自学算法

打赏

微信
支付宝

相关推荐

迭代、递归、时间复杂度、空间复杂度

数组、链表、列表

栈、队列、双向队列

数据库加载中